Find the Center and Radius x^2y^22x=0 x2 y2 − 2x = 0 x 2 y 2 2 x = 0 Complete the square for x2 −2x x 2 2 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = 0 a = 1, b = 2Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations (2x^2)/(xy)(5x^3y)/(xy) so that you understand betterSimple and best practice solution for x^2y^22x2y=34 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework

Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
(x^2+y^2+2x)dx+2ydy=0
(x^2+y^2+2x)dx+2ydy=0-Complete the square in x and y, The general equation for a circle centered at (,) with a radius is Comparing, (,)=(,)You can put this solution on YOUR website!




Tangents Pa And Pb Are Drawn To The Circle X2 Y2 8 From Any Arbitrary Point On The Line X Y 4 The Locus Of The Midpoint Of
90°, then find the value oयदि 2 cos 2 θ – 5 cos θ 2 = 0 है, और 0° θ ;X^2y^22x8y8=0 Found 2 solutions by Fombitz, solver Answer by Fombitz() (Show Source) You can put this solution on YOUR website!(xy)^2=(xy)(xy)=x{\color{#D61F06}{yx}} y=x{\color{#D61F06}{xy}}y=x^2 \times y^2\ _\square (x y) 2 = (x y) (x y) = x y x y = x x y y = x 2 × y 2 For noncommutative operators under some algebraic structure, it is not always true Let Q \mathbb Q Q be the set of quaternions, and let x = i, y = j ∈ Q x=i,y=j\in\mathbb Q x = i, y = j ∈ Q
A= 32/27 Consider the function f(x) = (x^22x4) (2x^24x3) f(x) = 3x^22x1 The values of x for which the two curves intersect are the solutions of the equation f(x) = 0 3x^22x1=0 x= (1sqrt(13))/3 x_1 = 1/3, x_2=1 Note now that as f(x) is a second degree polynomial with leading positive coefficient, its value is negative in the interval between the roots The areaHi, Showing graphically x^2y^22x2y=0 completing squares x^22x y^22y =0 (x1)^2 1 (y1)^2 1 = 0 (x1)^2 (y1)^2 = 2 x^2y^24x6y12=0 completing squaresDetermine whether or not F is a conservative vector field If it is, find a function f such that {eq}F = \triangledown f {/eq} {eq}a) \ F(x, y) = (2x 4y) i (4x
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us CreatorsMath Input NEW Use textbook math notation to enter your math Try itHInt 2 x 2 x (2 y) y 2 − 2 y 2 = 0 As x is real, the discriminant must be ≥ 0 (2 y) 2 − 8 (y 2 − 2 y 2) ≥ 0 0 ≥ − 4 (y − 2) 2 (y − 2) 2 ≤ 0 But as y is real, (y − 2) 2 ≥ 0




A Circle Has The Equation X 2 Y 2 2x 2y 2 0



How Do You Find The Area Of The Region Between The Curves Y X 1 And Y 2 2x 6 Socratic
Math Input NEW Use textbook math notation to enter your math Try itGet stepbystep solutions from expert tutors as fast as 1530 minutesFactor 2x^2xyy^2 2x2 − xy − y2 2 x 2 x y y 2 For a polynomial of the form ax2 bx c a x 2 b x c, rewrite the middle term as a sum of two terms whose product is a⋅c = 2⋅−1 = −2 a ⋅ c = 2 ⋅ 1 = 2 and whose sum is b = −1 b = 1 Tap for more steps Reorder terms 2 x 2 − y 2 − x y 2 x 2 y 2 x y



Otvety Mail Ru Kak Vyglyadit Grafik X 2 Y 2 2x




Solution Find The Equation Of The Normal To X 2 Y 2 5
X^2 y^2 2x 2y = 2 x^2 2x y^2 2y = 2 (x 1)^2 (y 1)^2 = 2 1 1 = 4 (x 1)^2 (y 1)^2 = 4 Circle with radius of 2Trigonometry Graph x^2y^22x2y1=0 x2 y2 2x 2y 1 = 0 x 2 − y 2 − 2 x − 2 y − 1 = 0 Find the standard form of the hyperbola Tap for more steps Add 1 1 to both sides of the equation x 2 y 2 2 x 2 y = 1 x 2 − y 2 − 2 x − 2 y = 1 Complete the square for x 2 2 x x 2 − 2 xPlot(y=2xx^2, y=x) Natural Language;



Search Q Desmos Tbm Isch



What Is The Equation Of The Diameter Of Circle X 2 Y 2 2x 4y 0 Which Passes Through Origin Quora
You can put this solution on YOUR website!The equation of the chord of the circle x 2 y 2 = 2 5 of length 8 that passes through the point (2 3 , 2) and makes an acute angle with the positive direction of the xaxis is View solution In the above figure E is any point on median A D of A B CFind the Center and Radius x^22xy^2=0 x2 − 2x y2 = 0 x 2 2 x y 2 = 0 Complete the square for x2 −2x x 2 2 x Tap for more steps Use the form a x 2 b x c a x 2 b x c, to find the values of a a, b b, and c c a = 1, b = − 2, c = 0 a = 1, b = 2



Quadratics
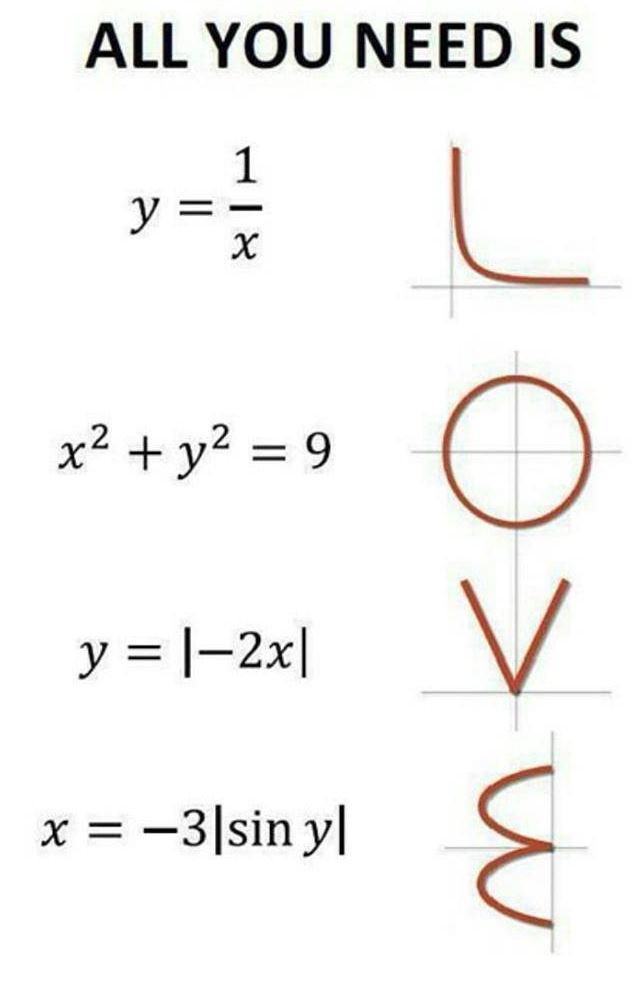



Manuel Barrera Y 1 X X2 Y2 9 Y 2x X 3 Sin Y
Y = x2 − 2x − 2 y = x 2 2 x 2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Complete the square for x 2 − 2 x − 2 x 2 2 x 2 Tap for more steps Use the form a x 2 b x c a x 2 b xIf 2 cos 2 θ – 5 cos θ 2 = 0, If 0° θ ;Click here👆to get an answer to your question ️ Find the equation of the tangents to the circle x^2 y^2 2x 4y 4 = 0 which are (i) parallel, (ii) perpendicular to the line 3x 4y 1 = 0




Tim Gtnn Của X 2 Xy Y 2 2x 2y Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải Bai Tập Toan Học Lớp 8 Lazi Vn Cộng đồng Tri Thức Giao Dục




Examine The Function F X Y 2x 2 2y 2 2x 4y Chegg Com
Equations Tiger Algebra gives you not only the answers, but also the complete step by step method for solving your equations 4(x^33x^2y2xy^2y^3)2x(3x^22xy5y^2) so that you understand betterGraph y=2xx^2 y = 2x − x2 y = 2 x x 2 Find the properties of the given parabola Tap for more steps Rewrite the equation in vertex form Tap for more steps Reorder 2 x 2 x and − x 2 x 2 y = − x 2 2 x y = x 2 2 x Complete the square for − x 2 2 x x 2 2 xY 2 2 y x 2 − 2 x − 3 = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2 for b, and \left (3x\right)\left (1x\right) for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a} This equation is in standard form a x 2 b x c = 0




The Parametric Equations Of The Circlex2 Y2 2x 4y 11 0 Are Brainly In




Find Equation Of Diameter Of Circle X 2 Y 2 2x 4y 0 Which Passes Through 3 4 Maths Meritnation Com
X = 2 − 2 − ( y − 2) 2 2 Divide 22\sqrt {\left (2y\right)^ {2}} by 2 Divide 2 − 2 − ( − 2 y) 2 by 2 x=\sqrt {\left (y2\right)^ {2}}1 x = − − ( y − 2) 2 1 The equation is now solved The equation is now solved x=\sqrt {\left (y2\right)^ {2}}1 x=\sqrt {\left (y2\right)^ {2}}1X=\frac {y2} {2} x = 2y −2 View solution steps Steps for Solving Linear Equation y=2x2 y = 2 x 2 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand sideWe think you wrote (3x)/(2x^23xy2y^2)(y)/(x^24y^2)(2xy)/(2x^25xy2y^2) This deals with adding, subtracting and finding the least common multiple




Tangents Pa And Pb Are Drawn To The Circle X2 Y2 8 From Any Arbitrary Point On The Line X Y 4 The Locus Of The Midpoint Of




Q 7 Show That The Circles X2 Y2 2x 2y 7 0 And X2 Y Gauthmath
The Beat The GMAT Forum Expert GMAT Help & MBA Admissions Advice A GMAT and MBA community featuring expert advice, free GMAT prep x=2,y=4 color(red)(y=x2)(1) y=2x2y(2) perhaps teh quickest way is to substitute (1)" into "(2) color(red)(x2)=2x2color(red)((x2)) x2=cancel(2x2x)4 Please see the explanation below The equation is x^2y^22x4y4=0 Complete the square x^22xy^24y=4 x^22x1y^24y4=414 Factorise (x1)^2(y2)^2=9=3^2 This is the equation of a circle, center C=(1,2) and radius r=3 The graph is shown below graph{(x^2y^22x4y4)=0 8065, 7735, 218, 572}



The Area In Sq Units Of The Region X Y Y 2 2x And X 2 Y 2 4x X 0 Y 0 Is Sarthaks Econnect Largest Online Education Community



Find The Point On A Circle X2 Y2 2x 4y 11 0
All equations of the form a x 2 b x c = 0 can be solved using the quadratic formula 2 a − b ± b 2 − 4 a c The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction x^ {2}2xy^ {2}2y=0 x 2 2 x y 2 2 y = 0 This equation is in standard form ax^ {2यदि x 2 y 2 z 2 = 2(x y z) – 3 है, तो (2x 3y 4z) का मान ज्;X²=9y² x²y²=9 x2y=2x²7x 2y=2x²7 y=x²7/2 x²(x²7/2)²=9 x²x^47x²49/4=9 x^48x²=36/4–49/4=13/4 Here's a screenshot of the graph of the two




C 1 X 2 Y 2 25 C 2 X 2 Y 2 2x 4y 7 0 Be Two Circle Intersecting At A And B Then



Solution I Need Help Graphing X 2 Y 2 2x 2y 2 I Also Need To Find The Intercepts
Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music The equation is invariant under the above scaling whenever α = ± β It means, It suggests the change of variables u ≡ y x y = u x Namely, You could treat 2 x y y ′ = x 2 − y 2 as homogeneous (after a bit of algebra) But this is an exact equation You have P = − x 2 y 2 and Q = 2 x y Notice that P y = 2 y = Q xSolve xy'y=2x WolframAlpha Assuming "solve" is a word Use as referring to equation solving



X 2 Y 2 1 0 Chaimmy
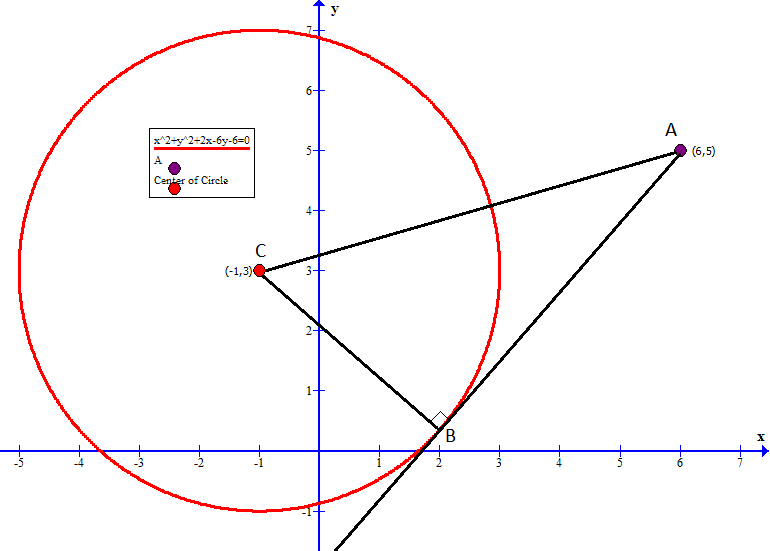



Given That A Circle Has An Equation Of X 2 Y 2 2x 6y 6 0 What Is The Exact Length Of Ab Given That A Tangent Is Drawn From A 6 5 And Touches The Circle At B Socratic
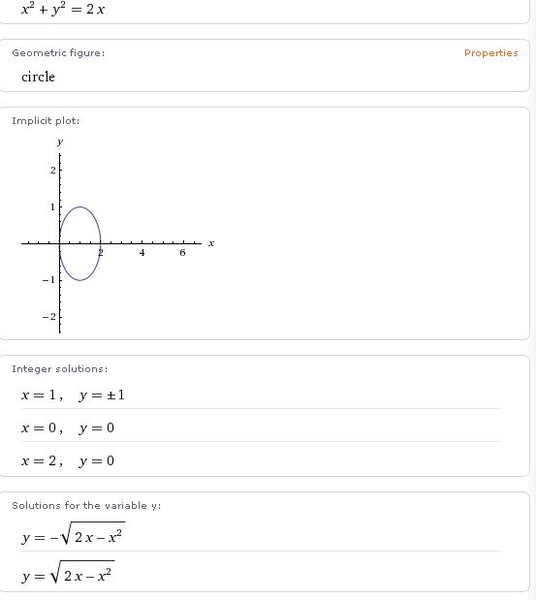
Algebra Simplify 2x^2x^2 2x2 − x2 2 x 2 x 2 Subtract x2 x 2 from 2x2 2 x 2 x2 x 2The area bounded between the parabolas x 2 = y/4 and x 2 = 9y and the straight line y = 2 is The area bounded by the curve y = 2x x 2 and the line y = x is The area bounded by the curve y 2 (2a x) = x 3 and the line x = 2a is The area bounded by the curves y = cos x and y = sin x between the ordinates x = 0 and x = 3π/2 is The area 2rcos theta = r^2 Substitute { (x= r cos theta), (y=r sin theta) } So we have 0 = x^2y^22x =(r cos theta)^2(r sin theta)^22r cos theta =r^2(cos^2 theta sin^2 theta) 2r cos theta =r^22r cos theta Add 2rcos theta to both ends and transpose to find 2rcos theta = r^2 graph{x^2y^22x=0 1667, 3333, 128, 122}



The Circle X 2 Y 2 2x 2y 1 0 Is Rotated About Its Point Of Contact With Y Axis Through The Angle Sarthaks Econnect Largest Online Education Community



Ellipses And Hyperbolae
That's a circle Compare mathx^2y^22x=0/math with the general equation of a circle mathx^2y^22gx2fyc=0/math and write down the values of the constantsTranscribed image text Consider xy" x(x2)y' (x2)y= 2x, x>0 Let the particular solution be y, = u(x));Combine all terms containing x Combine all terms containing x x^ {2}\left (2y8\right)xy^ {2}8y=0 x 2 ( − 2 y − 8) x y 2 − 8 y = 0 This equation is in standard form ax^ {2}bxc=0 Substitute 1 for a, 2y8 for b, and y\left (8y\right) for c in the quadratic formula, \frac {b±\sqrt {b^ {2}4ac}} {2a}




Ex 24 1 Q19 The Circle X 2 Y 2 2x 2y 1 0 Is Rolled Along The Positive Direction



How To Draw The Graph Of X 2 Y 2 2x 0 Quora
Since you can choose any value you like for x, pick something that will make the arithmetic simple 0 is always a good choice So our first point is (0,2), because we chose 0 for x, and that resulted in 2 for y Let's try x = 1 So the second point is (1,3), because we chose 1 for x, and that resulted in 3 for y Plot the points Then draw the lineExtended Keyboard Examples Upload Random Examples Upload RandomA Power consists of two parts, (z^32)/(x^2zy^2z)*z^2/(x1)*(2x^32xy^2)/(2xz^32xz^2) Exponent and Base, We are going to learn to identify components of a Power and



What Is X2 Y2




Tentukan Titik Potong Lingkaran L X2 Y2 2x 10y 24 Dengan Mas Dayat
V(x)y2, where y1 = x and Y2 = xe' are the solutions ofThe equation of the circle is x^2y^22x2y14=0 Write this in the standard form of a circle with center (h, k) and radius r (x h)^2 (y k)^2 = r^2 x^2y^22x2y14=0Sign up for a free account at https//brilliantorg/blackpenredpen/ and try their daily challenges now You can also get a % off discount for their annual
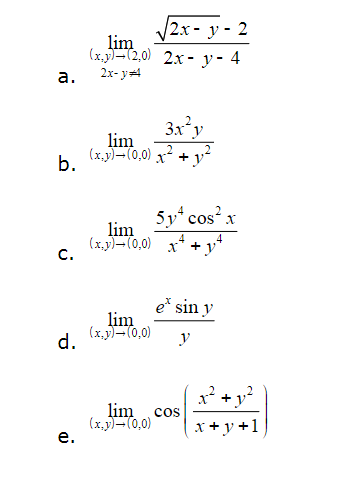



2x Y 2 2x Y 4 Xy 12 0 Lim X Y 0 0 X2 1 2 Chegg Com
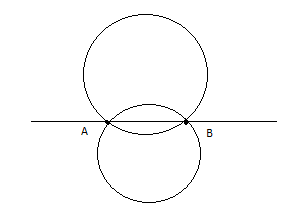



Determine Equation Of The Circle Whose Diameter Is Class 12 Maths Cbse
X^2 2 y^2 = 1 Natural Language;How prove this BC always passes through a fixed point with \frac{x^2}{4}y^2=1 How prove this B C always passes through a fixed point with 4 x 231 Factoring 2x 2y Theory A difference of two perfect squares, A 2 B 2 can be factored into (AB) • (AB) Proof (AB) • (AB) = A 2 AB BA B 2 = A 2 AB AB B 2 = A 2 B 2 Note AB = BA is the commutative property of multiplication Note AB AB equals zero and is therefore eliminated from the expression Check 2




The Circle C Has Equation X2 Y2 2x 14y 0 Find A Th Gauthmath




All You Need Is X2 Y2 9 Y L 2xl X一一3lsiny 3 Sinyl I Y 1x X 2 Y 2 9 Y 2x X 3 Sin Y Youuuuuu Smile Smile Meme On Awwmemes Com
Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historySee the entire solution process below Explanation Step 1) Solve the first equation for x 2 x 3 y = 1 6 2 x 3 y − (3 y) = 1 6 − (3 y) 2x3y=23 2 x 3 y = 2 3



Www Lcps Org Cms Lib Va Centricity Domain 2 5 notes filled out Pdf




Let F X Y Xy X 2 Y 2 2x 2y 4 Find The Chegg Com




If One Of The Diameters Of The Circle X 2 Y 2 2x 6y 6 0 Is A Chord To The Circle With Centre 2 1 Then Radius Of The Circle Is Ans 3
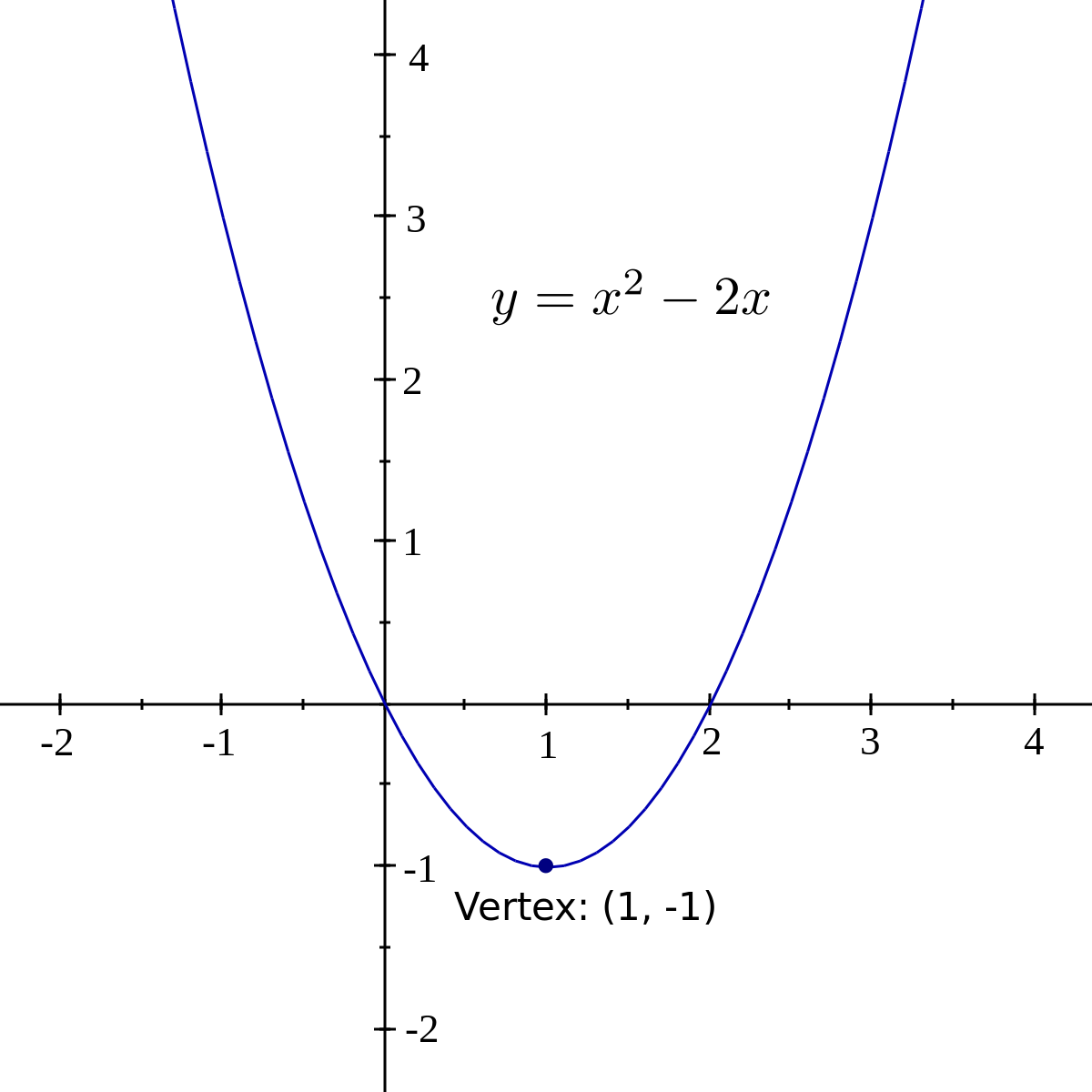



File Y X 2 2x Svg Wikimedia Commons




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange
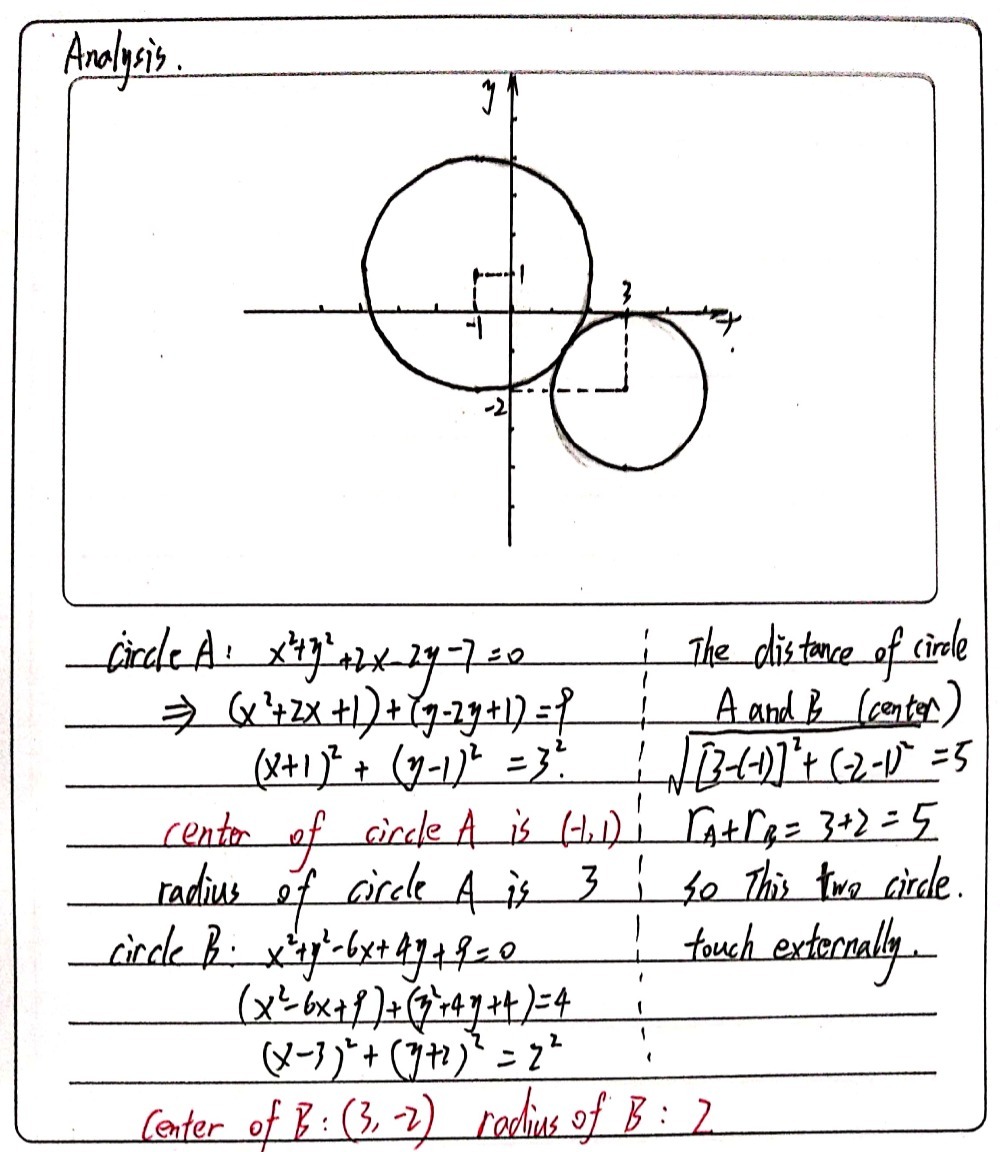



Fbd 15 Show That The Circle X2 Y2 2x 2y 7 0 An Gauthmath




Factorise X 2 Y 2 2x 4y 1 4 Brainly In




Find The Minimum Value Of 2x 2 2xy Y 2 2x 2y 3 Msrblog



File Y X 2 2x Svg Wikimedia Commons




Sketch The Region Enclosed By The Curves Y 2 2x 6 And Y X 1 And Find The Area Youtube
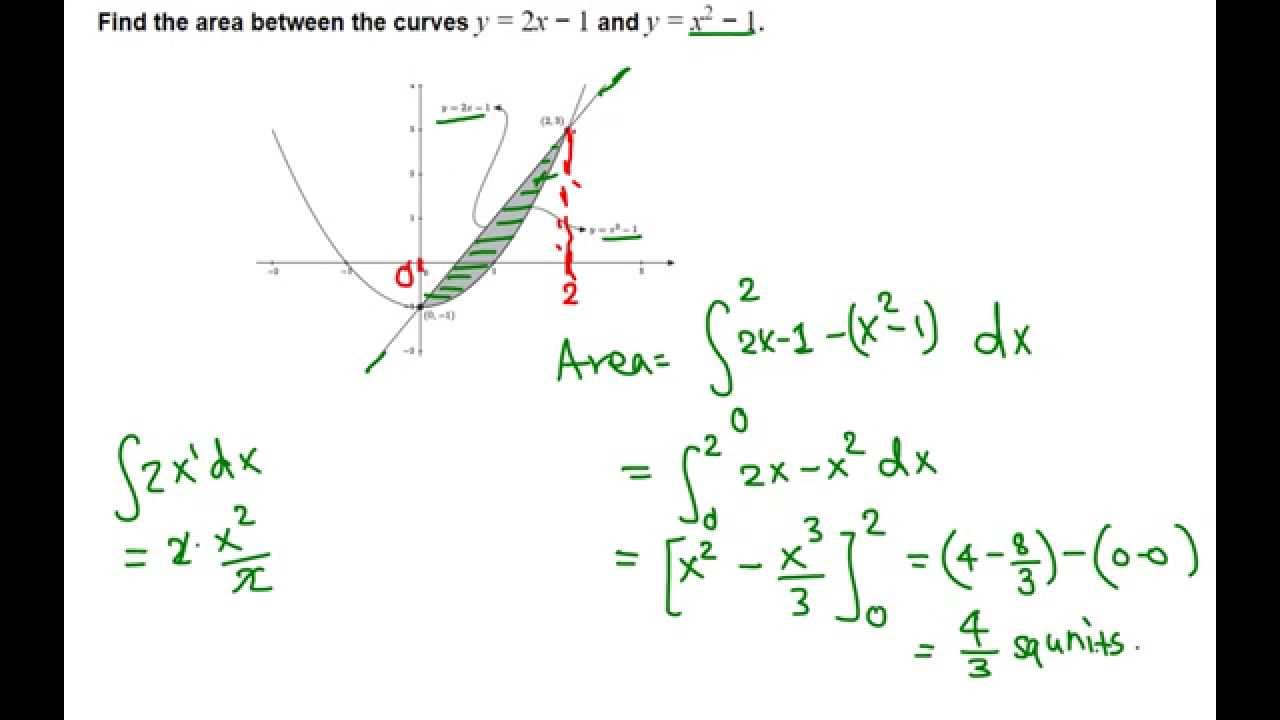



Area Between Y 2x 1 And Y X 2 1 Youtube
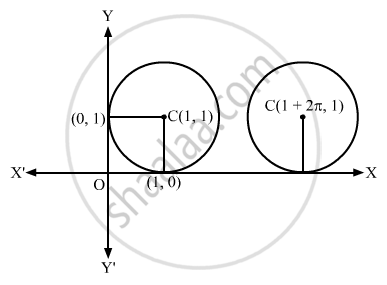



The Circle X2 Y2 2x 2y 1 0 Is Rolled Along The Positive Direction Of X Axis And Makes One Complete Roll Find Its Equation In New Position Mathematics Shaalaa Com




X 2y 3 2 2x Y 3 2 Find The Valve Of X And Y Brainly In




If 2x 2 2y 2 2x 2y 1 0 Then What Is The Value Of X Y Quora




If Y Tan 1 X 2 Show That X2 1 2 Y2 2x X2 1 Y1 2 Mathematics Shaalaa Com
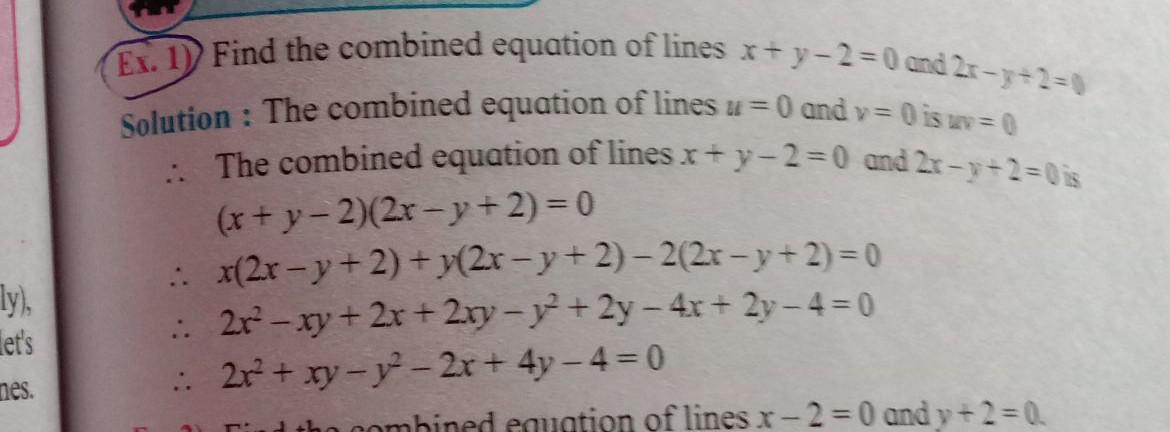



Find The Combined Equation Of Lines X Y 2 0 And 2 Math




Evaluate The Double Integral Iint C Sqrt 4 X 2 Y 2 Dxdy Bounded By Semi Circle X 2 Y 2 2x And Lying In First Quadrant Study Com




Factorise X 2 Y 2 2x 1




If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk



1




Btech Ii Engineering Mathematics Unit3




The Radius Of The Circle In Which The Sphere X2 Y2 Z2 2x 2y 4z 19 0 Is Cut By The Plane X 2y
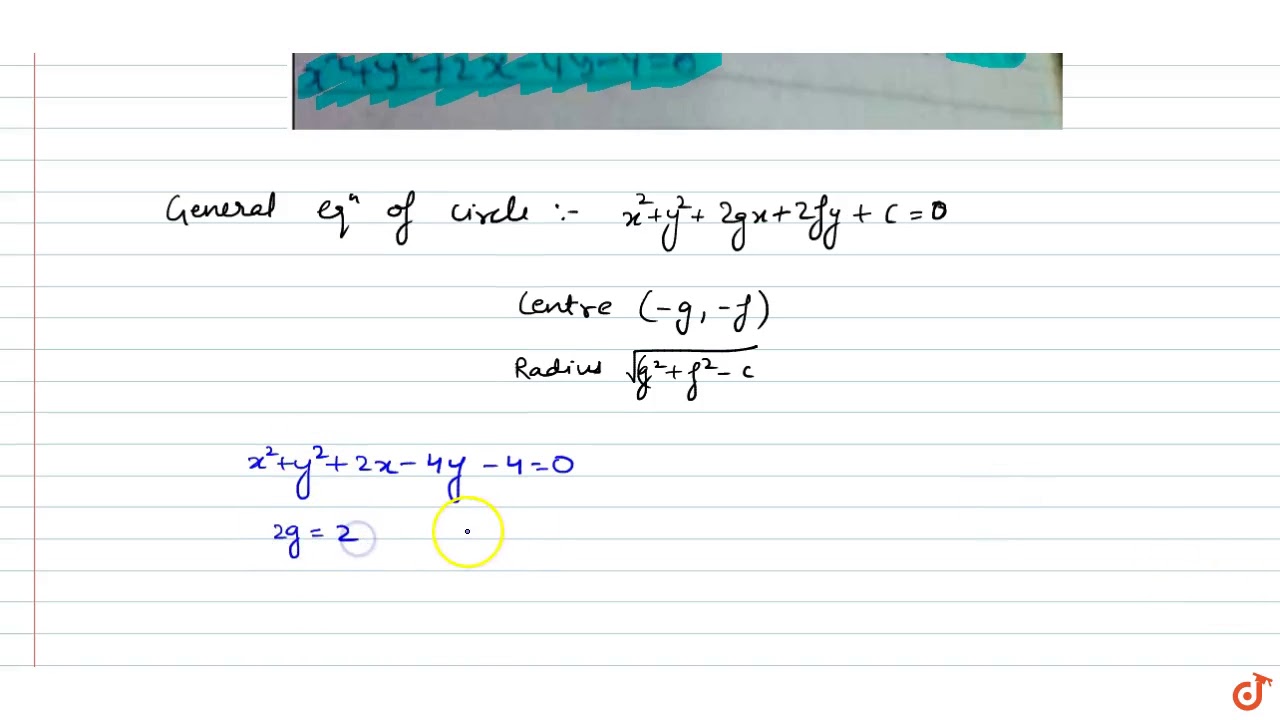



Find The Centre And Radius Of The Circle X 2 Y 2 2x 4y 4 0 Youtube




Show That The Circle X2 Y2 2x 2y 1 0 And X2 Y2 6x 4y 3 0 Touch Each Other Externally Brainly In




Prove That The Radio Of The Circles X 2 Y 2 1 X 2 Y 2 2x 6y 6 0 And X 2 Y 2 4x 12y 9 0 Are In Ap Mathematics Topperlearning Com Sq29gmm




Warm Up Exercises Factor 1 X 2 2x 48 Answer 8 X 6 Ppt Video Online Download
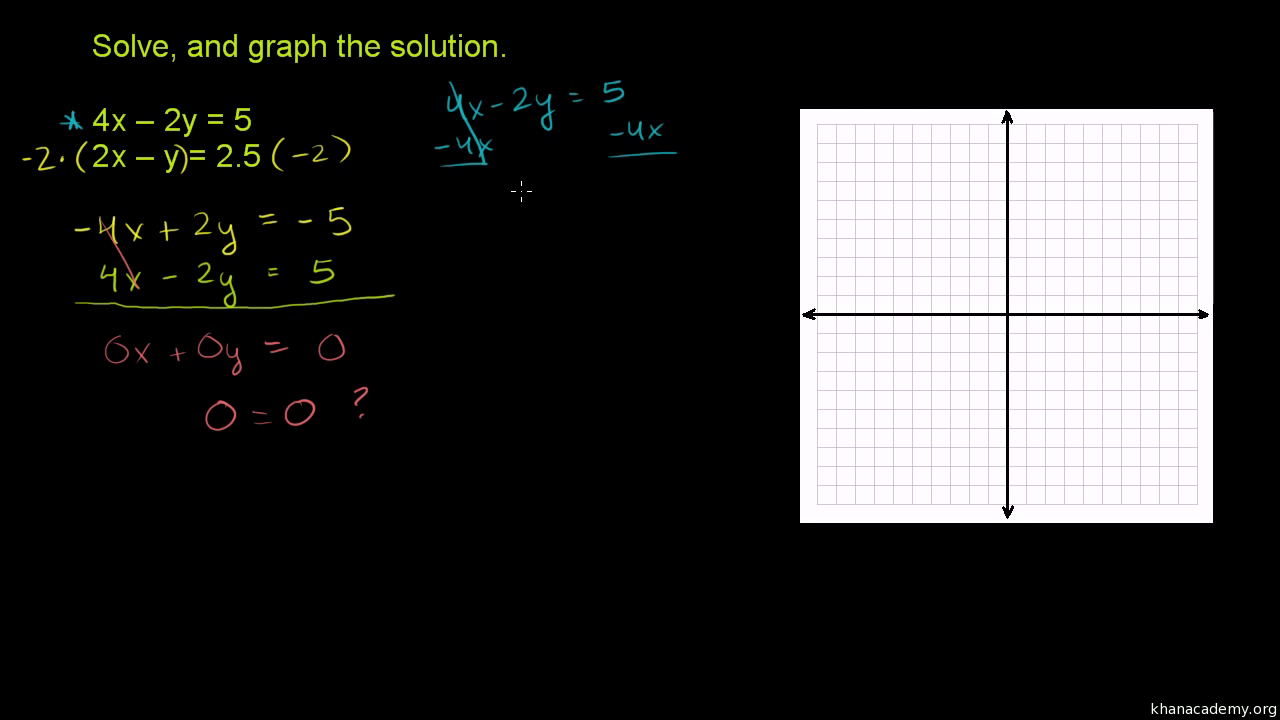



Systems Of Equations With Elimination 4x 2y 5 2x Y 2 5 Video Khan Academy
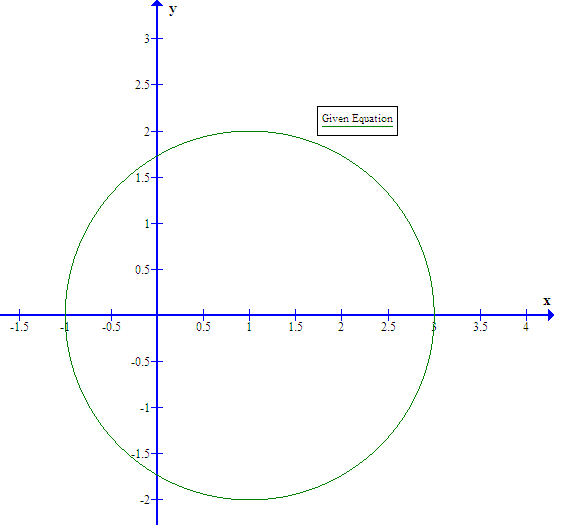



How Do You Find The Center And Radius Of The Circle X 2 Y 2 2x 3 0 Socratic



1
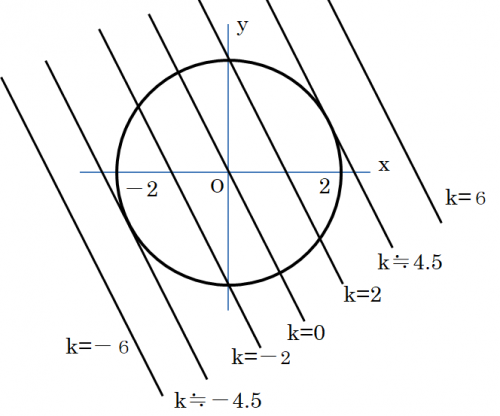



実数x Yはx 2 Y 2 4を満たすとき2x Yの最大値と最小値を求めよ という 数学 教えて Goo



Solution Find The Center Of A Circle With The Equation X2 Y2 2x 4y 9 0
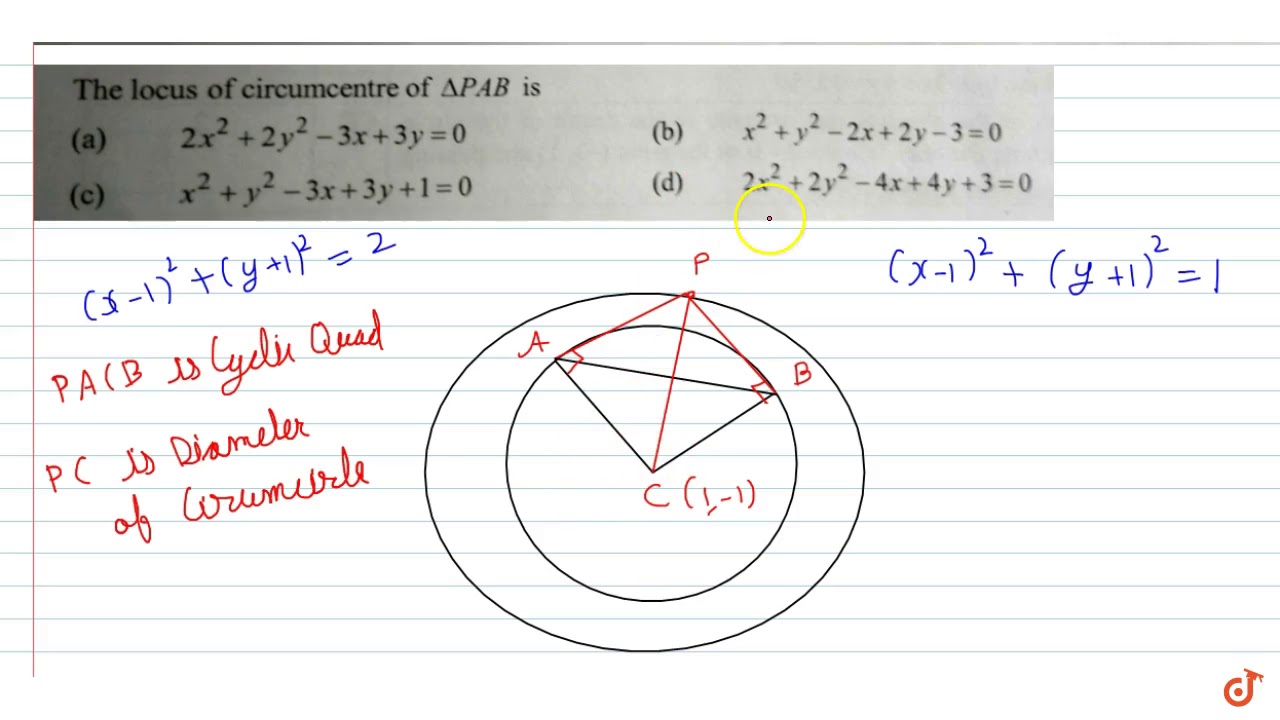



Let C 1 X 2 Y 2 2x 2y 0 And C 2 X 2 Y 2 2x 2y 0 Are Two Given Circles From A Mov Youtube
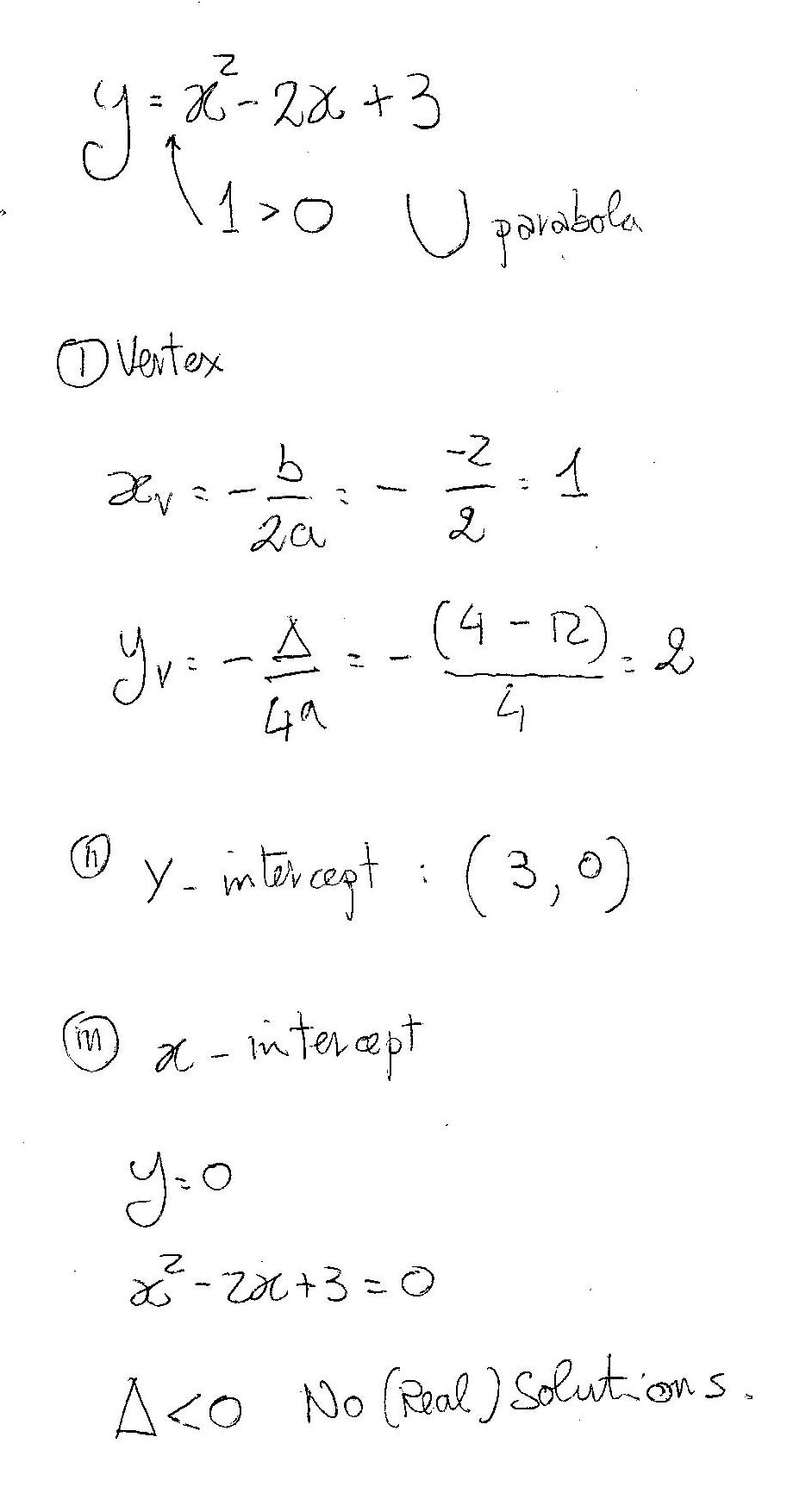



How Do You Graph Y X 2 2x 3 Socratic
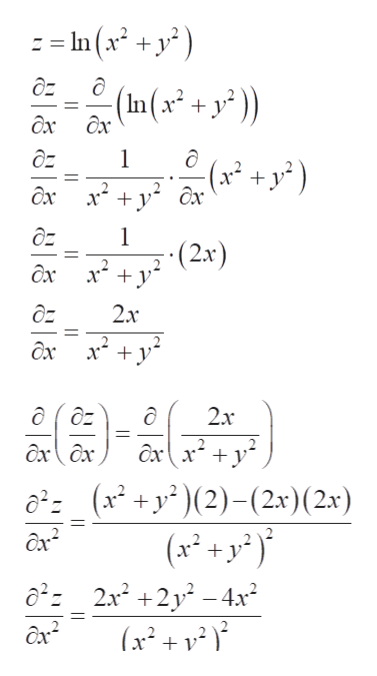



Answered Show That F X Y Ln X2 Y2 Solves Bartleby
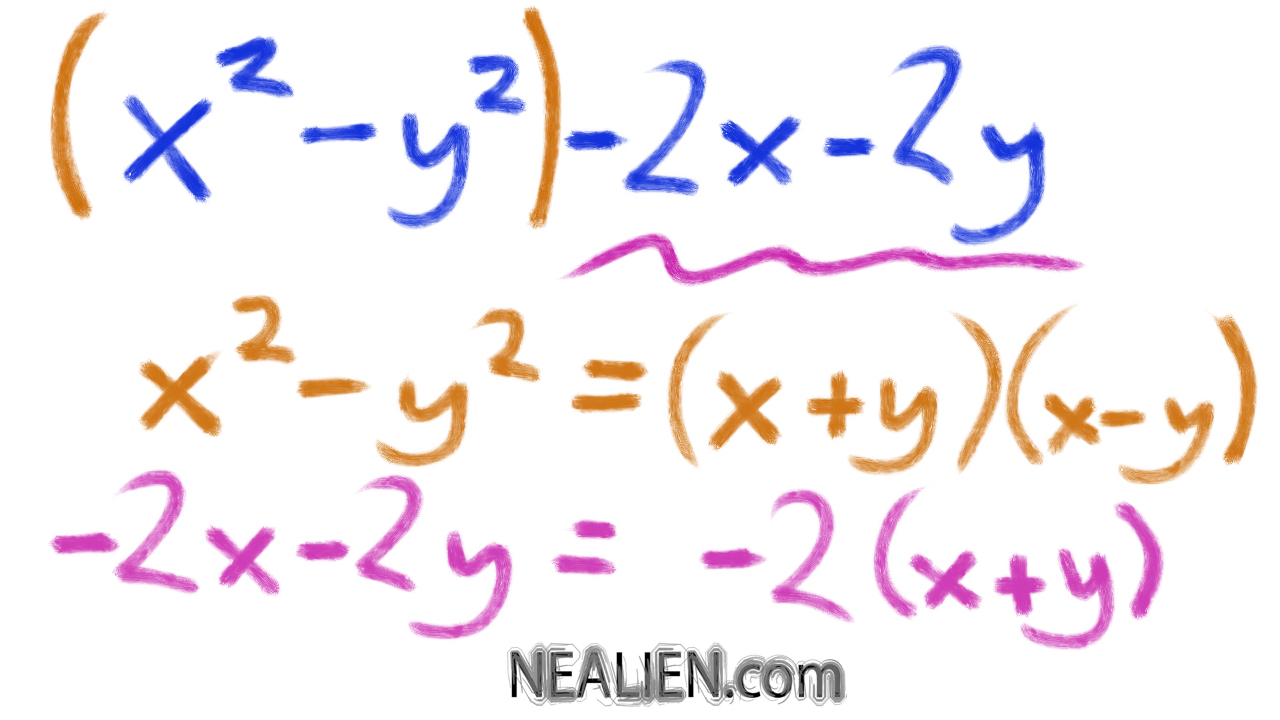



How Do You Factor The Following Expression Math X 2 Y 2 2x 2y



At What Points On The Curve X 2 Y 2 2x 4y 1 0 The Tangents Are Parallel To The Y Axis Sarthaks Econnect Largest Online Education Community



Let A Be The Centre Of The Circle X 2 Y 2 2x 4y 0 Suppose That The Tangents At The Points B 1 7 Sarthaks Econnect Largest Online Education Community




Reshit Sistemu Uravnenij X Y 2 X 2 Y 2 2x 0 Shkolnye Znaniya Com
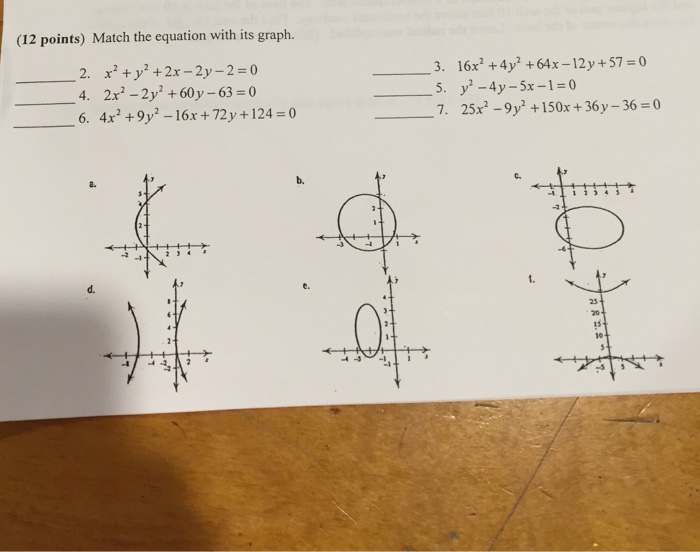



Match The Equation With Its Graph 2 X 2 Y 2 Chegg Com
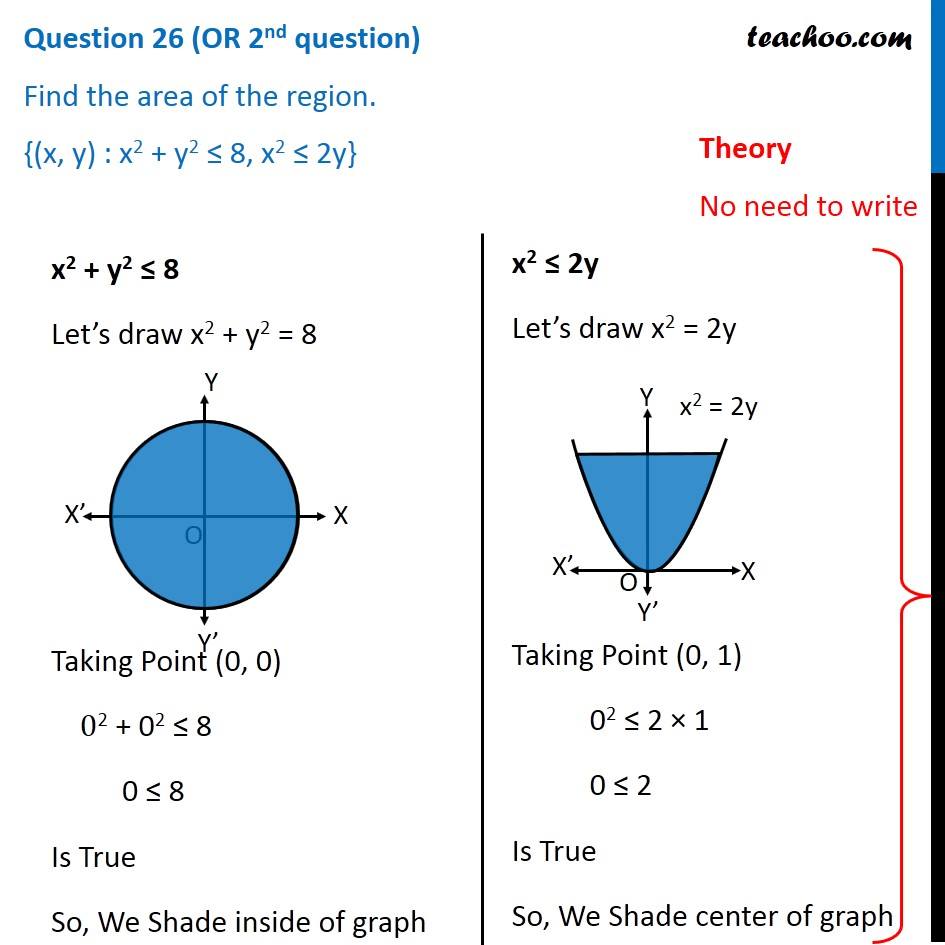



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y




X 2 Y 2x 2 Y 2 4xy Y 1 1 Xyy 3x 2 Chegg Com




Solution What Are The Coordinates Of The Center Of The Curve X 2 Y 2 2x 4y 31 0




4 X 2 2x Y 2 8 4 Example 6 Classify A Conic Classify The Conic Given By 4x 2 Y 2 8x 8 0 Then Graph The Equation Solution Note Ppt Download




Find The Products I 2x Y 2x Y 4x 2 Y 2 Ii X Y 5 1 X Y 5 1



How To Factorise X 2 2x Y 2 2y Quora




Image Of The Curve X 2 Y 2 1 In The Line X Y 1 Is Youtube



Solution The Circle X 2 Y 2 2x 3 0 Is Stretched Horizontally By A Factor Of 2 About X 0 To Obtain An Ellipse What Is The Equation Of This Ellipse In General Form




Factorise X2 Y2 2x 1 Maths Polynomials Meritnation Com




The Circle X 2 Y 2 2x 2y 1 0 Is Rolled Along The Positive Direction Of X Axis And Makes One Youtube



Compute The Area Bonded By The Lines X 2y 2 Y X 1 And 2x Y 7 Studyrankersonline




15 2xy Y 2 Dx 2xy X 2 2x 2y 2 2xy 3 Dy 0 Homeworklib




Find The Points On The Curve X2 Y2 2x 3 0 At Which The Tangents Are Parallel To The X Axis Mathematics Shaalaa Com




245 Given Three Circles X2 Y2 3x 6y 14 0 X2 Y2 X 4y 8 0 And X Y2 2x




Solution What Are The Coordinates Of The Center Of The Curve X 2 Y



At What Points On The Curves X2 Y2 2x 4y 1 0 The Tangents Are Parallel To The Y Axis Studyrankersonline
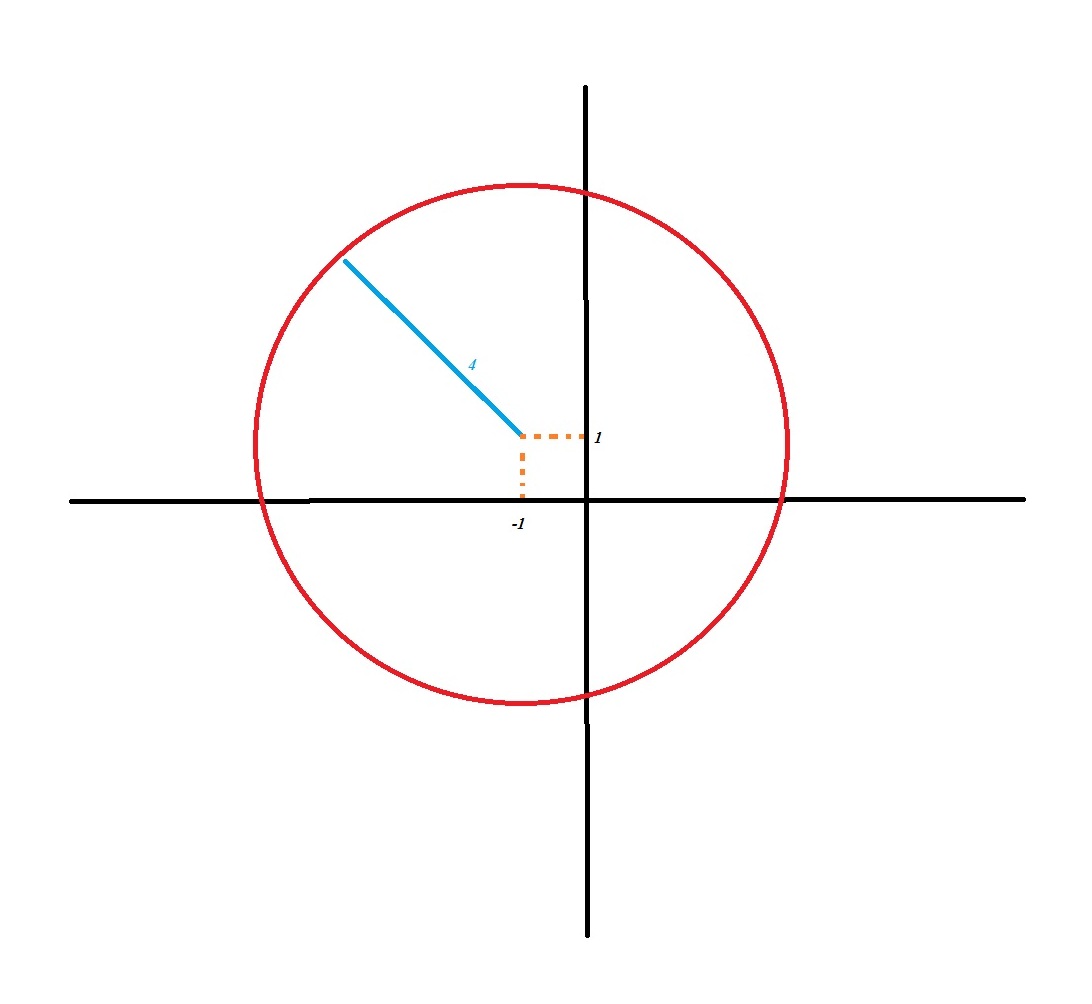



Circle Has The Equation X 2 Y 2 2x 2y 14 0 How Do You Graph The Circle Using The Center H K Radius R Socratic
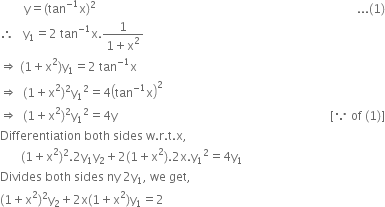



If Y Tan 1 X 2 Then Prove That 1 X2 2 Y2 2x 1 X2 Y1 2 From Mathematics Continuity And Differentiability Class 12 Up Board




Ex 9 5 15 Class 12 Find Solution 2xy Y 2 2x 2 Dy Dx 0 When




Solve For X And Y 2 2x Y 1 X 2y 5 9 0 9 2x Y 6 X 2y 4 0 Maths Pair Of Linear Equations In Two Variables Meritnation Com




Otvety Mail Ru Pomogite S Sistemkami 1 X 2 Y 2 2x Y 2 2 X 2 2 X 2 2x 1 2 Lt 0 X 1 Lt 1




Evaluate The Iterated Integral By Converting To Polar Coordinates 2 0 Sqrt 2x X2 0 6 Sqrt X2 Y2 Dy Dx Studentshare




4 If The Angle Between The Circles X2 Y2 2x 4y C 0 And X2 Y2 4x 2y 4 0 Is 60 Then C Is Equal A P Eamcet 16 0 1 34v5 2 6 V5 3 9395 4 7



Implicit Differentiation



X 2 Y 2 2x 8y 8 0 Mathskey Com




Ex 6 3 19 Find Points On X2 Y2 2x 3 0 Tangents
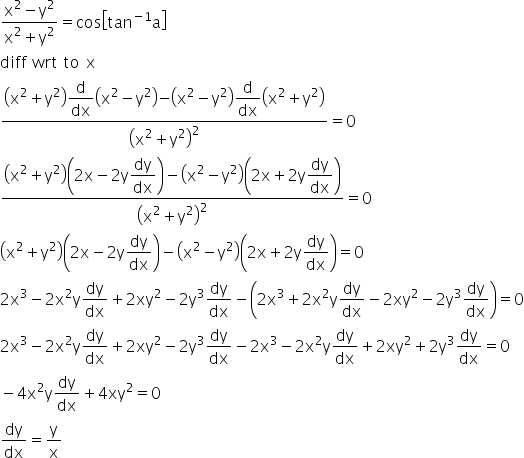



If Cos 1 X2 Y2 X2 Y2 Tan 1 A Prove That Dy Dx Y X Mathematics Topperlearning Com K6vhyqq
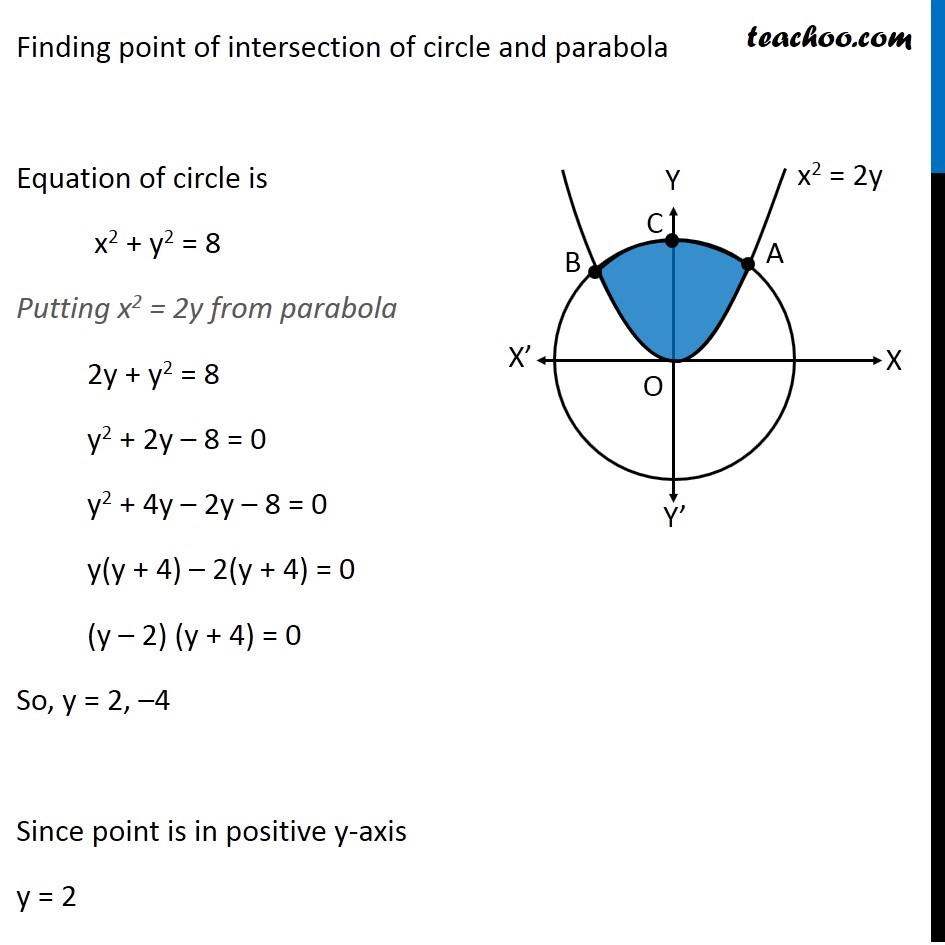



Find The Area Of The Region X Y X 2 Y 2 8 X 2 2y



1




What Is The Parametric Equation Of The Circle X 2 Y 2 2x 4y 4 0 Maths Introduction To Three Dimensional Geometry Meritnation Com




Phan Tich đa Thức Thanh Nhan Tử X 2 Y 2 2x 2y Toan Học Lớp 8 Bai Tập Toan Học Lớp 8 Giải Bai Tập Toan Học




Reshite Sistemu Uravnenij 1 Y X 2 4y X 2 8 2 Y 2 2x 4y 8 2y X 2 3 X 2 Y 3 X Y Shkolnye Znaniya Com




X 4 X 2 Y 2 2x 2 Y Xy 2 Y 2 0 Download Scientific Diagram




Show That The Circles S X 2 Y 2 2x 4y 0 S X 2 Y 2 6x 2y 90 0 Touch Each Other Internally Find Their Point Of Contact




Solve Y 2 2x 2y Dx 2x 3 Xy Dy 0 Mathematics Stack Exchange



0 件のコメント:
コメントを投稿