This must mean that q is false and p ∧ (p → q) is true (if we want A → B to be false, we need A true and B false) Hence both p and p → q are true But this gives q true, which is a contradiction This technique is particularly slick for three'variable' statements as it saves you doing a giant 8row truth tableSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forQ)_r por ejemplo, aplicando modus ponens a p y p !

Geo Trans 15 Pdf Txt
P+q=q+p propiedad y ejemplo
P+q=q+p propiedad y ejemplo-Isten dos enteros p y q, q 6= 0, tales que r = p/q Un n´umero real que no es racional es irracional Ejemplo 8 Demuestre que la suma de dos racionales es un racional p Sean r y s racionales, si r es racional entonces r = p/q para q 6= 0 y si s es racional entonces s = t/u para u 6= 0 (hip´otesis) q Hay que demostrar que rs es racionalIntrodución a la Lógica por Stefan Waner y Steven R Costenoble 2 Lógica Equivalente, Tautologia, y Contradición Hemos sugerido en la sección previaque ciertas proposiciones son equivalentes Por ejemplo, decimos que (p q) r y p (q r) son equivalentes — un hecho al que llamamos la ley asociativo de la conjugación En esta sección, usamos tablas de verdad para decir precisamente




Lmf T1 Sintaxis Y Semantica De La Logica Proposicional Pdf Document
EJERCICIOS DE SIMPLIFICACION DE ECUACIONES LOGICAS 1 7 Leyes del Condicional a) p → q ≡ ~p ٧ q b) ~ (p → q) ≡ p ٨ ~q 8 Leyes del Bicondicional a) p ↔ q ≡ (p → q) ٨ (q → p) b) p ↔ q ≡ (p ٨ q) ٧ (~p ٨ ~q) 10 Leyes de Transposición a) (p → q) ≡ (~q → ~p) b) (p ↔ q) ≡ (~q ↔ ~pP q P ↔ q Bicondicional o doble implicación Si ingresa a la facultad, aprobó el ciclo básico Y si aprueba el ciclo básico, ingresa a la facultad P q q p (p q) ∧ ( q p) Así como en las proposiciones condicionales vimos que hay casos de condicionales contraPor lo tanto, p;
Ejemplo 1 Sea la proposición (x∧y) ∨ (x∧~y) Comparándola con la regla distributiva 4b, vemos que tenemos la parte derecha de ella si consideramos x = p, y = q, y ~y = r Por tanto, la proposición es equivalente a x ∧ (y∨~y) De la regla de identidad 7a tenemos que y∨~y = V, por tanto, la expresión es equivalente a11 PROPOSITIONS 7 p q ¬p p∧q p∨q p⊕q p → q p ↔ q T T F T T F T T T F F F T T F F F T T F T T T F F F T F F F T T Note that ∨ represents a nonexclusive or, ie, p∨ q is true when any of p, q is true and also when both are true On the other hand ⊕ represents an exclusive or, ie, p⊕ q is true only when exactly one of p and q is true 112Introducción Cálculo Las Matemáticas del cambio El término Cálculo identifica un conjunto de instrumentos matemáticos para efectuar medidas El Cálculo Diferencial trata de la medida de tasas de variación objetos en movimiento, crecimiento de seres vivos, transmisión de calor, campos electromagnéticos y un largo etcétera Por su parte, el Cálculo Integral, trata de medidas de
Y el tercer argumento, a pesar de no ser válido, se puedeQ ^r)!(p !(q !┐(P Q) = ┐P ┐Q Ejemplo ┐(A B) "Los murciélagos no son aves y el sol brilla" La condicional de P a Q es la proposición que afirma que si se cumple P entonces se cumple Q, se denota por P → Q y se lee "si P entonces Q" Ejemplos A → C "Si los murciélagos son




2 Taller De Conjuntos Docx Propiedades De Las Operaciones Entre Conjuntos Ley Conmutativa A Pq Qp B Puq Qup Ley Del Complemento A P P U19 B P P U19 Course Hero




Logica Proposicional Conceptos Basicos Algebra Pre Pdf
Condicional p →q = ~p v q p → q = ~q → ~p Bicondicional p ↔ q = (p → q) ^ (q → p) Dominancia p ^ F = F p v V = V Elemento Neutro p ^ V = P p v F = P 25 IMPLICACIÓN LÓGICA (A → B) Sean A y B dos formas proposicionales se dice que A implica lógicamente a B si y solo si A→B es una tautología, ejemplo Decir entre lo que sigue Explicación en video sobre las propiedades de la Suma de Polinomios Vídeo de CommentsR))(a1) Utilizando tableros semanticos´




Logica Proposicional Ing Nerio Villalobos Finol Pdf Free Download



Www Karlstorz Com Cps Rde Xbcr Karlstorz Assets Assets Pdf
El enunciado siguiente es una proposición bicondicional "Es buen estudiante4 TEMA 0 INTRODUCCION A LA L¶ OGICA¶ 03 Implicaciones y Equivalencias L¶ogicas Cuando dos f¶ormulas bien formadas P y Q tienen siempre los mismos valores de verdad, es decir, cuando el bicondicional P $ Q es una tautolog¶‡a, se dice que P y Q son l¶ogicamente equivalentes y se denota P QCapítulo 2 Álgebra Autores José Antonio Encabo de Lucas y Eduardo Cuchillo LibrosMareaVerdetk Revisor Luis Carlos Vidal Ilustraciones Banco de Imágenes de INTEF Álgebra 46 Ejemplo Dado el polinomio 6 3 2 2 4 − ≡ x x p y el polinomio 7 6 7 2 4 − ≡ x x q Vamos a restar p − q El proceso es el mismo que para la suma



Reglas De Inferencia Docsity




Tablas De Verdad Y Conectivos Logicos Ejercicios Resueltos Pdf
El elemento p representa un párrafo Se considera párrafo a un bloque de texto compuesto de una o más oraciones que se refieren a un tema en particular y que normalmente se separa de otros por un espacio en blanco Los autores no deberían utilizar al elemento p en ocasiones en que otros elementos más específicos, como address o blockquoteEn otro caso, p ∧ q es falsaEjemplo 1 Sea la fórmula F= (p q) q p y la interpretación I que asigna V I (p)=F y V I (q)=V Entonces V I (F)=V Definición 3 Una interpretación I es un modelo para una fórmula F si V I (F)=V Es posible establecer una clasificación de las fórmulas proposicionales en función de los valores que




01 Conceptos Basicos De Logica Matematica 5




Propiedades De Los Numeros Reales
Cornejofernando609 cornejofernando609 Matemáticas Bachillerato contestada Propiedad y ejemplo a) pq=qp 1 Ver respuesta cornejofernando609 está esperando tu ayuda Añade tu respuesta y gana puntos(q_r) , (p !Veri que las siguientes equivalencias usando propiedades conocidas Tambi en usando tablas de verdad (a) p !




Ejemplo Mostrar Que P Q V F Ppt Descargar



Www2 Ulpgc Es Hege Almacen Download 46 Logica Pdf
Aplicación de la leyes o propiedades de los exponentes en la potenciación para simplificar expresiones Ejercicios resueltos de potencias de igual base y potAnswer choices PropiedadYa vimos que p→q no es lo mismo que q→p Puede ocurrir, sin embargó, que ambos p→q y q→p son verdaderas Por ejemplo, si p "0 = 1" y q "1 = 2," entonces p→q y q→p ambas son verdaderas porque p y q ambas son falsas La proposición p↔q se define como la proposición (p→q) (q→p)




1 Proposiciones Logicas La Lgica Proposicional O Tambin




Resumen Algebra 1 Logica Proposicional Studocu
Subf(F) que calcula el conjunto de las subfórmulas de la fórmula F Por ejemplo, Subf(p !q _p) = fp !q _p, p,q _p,q,qg Ejercicio 13 Demostrar por inducción que todas las fórmulas proposicionales tienen un número par de paréntesis 7 8 Tema 1 Sintaxis y semántica de la lógica proposicionalForma Lógica p↔p 2 Principio de Nocontradicción No es posible que una proposición sea verdadera y falsa al mismo tiempo Forma Lógica ~ (p∧~p) 3 Principio de Tercio Excluido Toda proposición es necesariamente verdadera o necesariamente falsa No existe una posibilidad intermedia Forma Lógica p∨~p 4Sean p y q dos proposiciones entonces se puede indicar la proposición bicondicinal de la siguiente manera p « q Se lee "p si solo si q" Esto significa que p es verdadera si y solo si q es también verdadera O bien p es falsa si y solo si q también lo es Ejemplo;
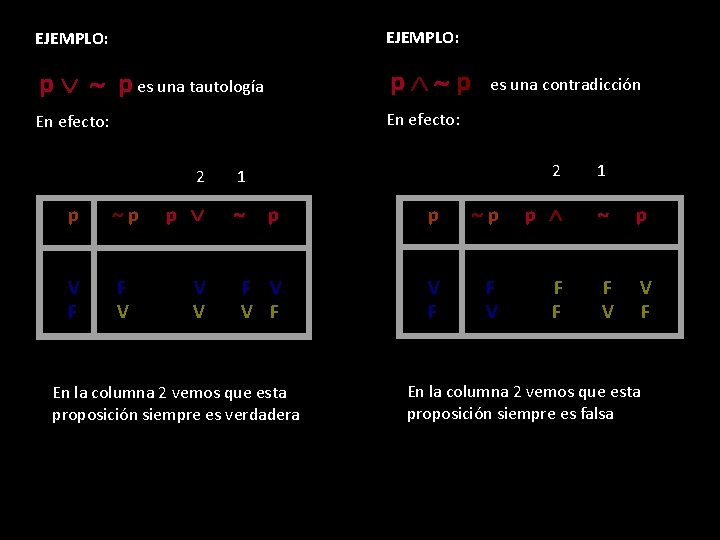



1 Proposiciones Logicas La Lgica Proposicional O Tambin




Logica De Primer Orden Monografias Com
Haz clic aquí 👆 para obtener una respuesta a tu pregunta ️ p(qr)=(pq)r ejemplo y propiedad estefaniab912 estefaniab912 Matemáticas Universidad contestada P(qr)=(pq)r ejemplo y propiedad 1 Ver respuesta Publicidad Publicidad estefaniab912 está esperando tu ayuda Añade tu respuesta y gana puntosPor ejemplo, si p es el 6 es un numer¶ o par, sp ser¶a el 6 no es un numer¶ o par Luis Zegarra A Introducci¶on a la l¶ogica matem¶atica y a la teor¶‡a de conjuntos 4 Deflnici¶on Sean p y q dos proposiciones, deflniremos las proposiciones sp, p^q, p_q y p_q mediante las llamadas tablas de verdad p q sp p^q p_q p_q V V F V V F VEjemplo 8 Si p(x) = 2x3 3x2 1 y q(x) = x4 x2 x son como en el ejemplo 3 entonces p(x) 2x3 3x2 1 Recordemos que para multiplicar dos polinomios, esencialmente aplicamos la propiedad distributiva y las propiedades de la potencia de nu´meros complejos Veamos un ejemplo Ejemplo 9 p(x) = x5 −ix2 2x y q(x) = x2 3, entonces




Diseno Del Logotipo De La Letra De Qp Qp Con Las Llamas Del Fuego Y El Ejemplo Anaranjado Del Vector De Swoosh Ilustraciones Vectoriales Clip Art Vectorizado Libre De Derechos Image



2
(q_r) se in ere q_r, y no parece haber otra deducci on m as \corta" As se tiene Si p, q y r tienen valores de verdad V, F y V respectivaAmplio alcance de proposiciones en matemáticas y ciencias de cómputosde manera que nos permite razonar y explorar relaciones entre los objetos I Predicados Es una propiedad ó característica del sujeto P(x) se llama la función proposicional P de x Ejemplo # 1 "x > 3", " x = y z", "computadora x está bajo el ataque de unProposiciones Llamaremos proposiciones a aquellas frases del lenguaje natural, las cuales podamos afirmar que son verdaderas o falsas Ejemplos de proposiciones Dos es par Tres es mayor que diez Tres más cuatro es nueve 3 Una proposición es simple o atómica, si ninguna parte de ella es a su vez una proposición




Antecedentes
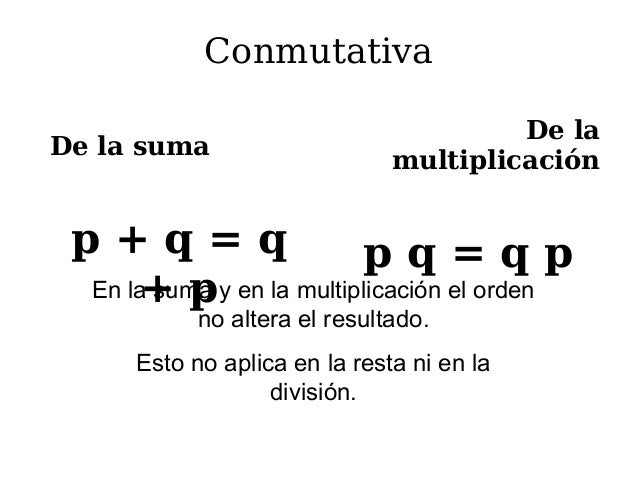



Propiedades
Con Tablas de la Verdad se analiza una Proposición Lógica para saber si es una tautologia o contradicción o contingencia Más videos sobre LÓGICA https//w Disyunción Si p y q son proposiciones, se llama disyunción de p y q a la proposición compuesta "p o q" y se denota por p q p q p q V V V V F V F V V F F F 17 Disyunción Seré cantante o futbolista p Seré cantante q Seré futbolista Simbolización p q p q p q V V V V F V F V V F F F 18Propiedad y ejemplo de pq=qP Pide más detalles ;




Base B Diagonal D Squared Diagonal D 2 Simplified Base B Simplified Download Table




Propiedades De Los Numeros Reales Ppt Video Online Descargar
Filosofía y Ciudadanía – Lógica proposicional Ejercicios resueltos 3 5 Enlaza cada proposición con su formalización "Llueve" = p, "Hace sol" = q, "Las brujas se peinan" = r 1 Llueve y hace sol 1A p ∧∧∧∧ q 2 No es cierto que si llueve y hace sol las brujas se peinan 3B r ↔ (p ∧∧∧∧q) 3 Las brujas se peinan únicamente si llueve y hace sol 4C ¬r → ( ¬p4 Examen de Diciembre de 00 Examen de Diciembre de 00 Ejercicio 1 El ejercicio consta de dos apartados (a) Probar que la siguiente formula es una tautolog´ ´ıa (p !Propiedad DCiv Derecho real que consiste en el grado máximo de poder sobre una cosa de la que se es titular El CC lo define en término s absolutos como «derecho de gozar y disponer de una cosa sin más limitaciones que las establecidas por las leyes», pero el art 33 CE, además de reconocerlo como derecho fundamental, establece que la




Atomistic Simulation Studies Of The Cement Paste Components




Logica Matematica Pptx Powerpoint
A estas letras se las llama variables proposicionales, y en general se toman del alfabeto latino, empezando por la letra p (de «proposición») luego q, r, s, etc Es así que los dos primeros argumentos de esta sección se podrían reescribir así p o q;Seguir camion para transladar los productos a sus localidades el camion llevo los viveres a la municipalidad A donde descargo y entrego al responsable del almacen los productos para luego dirigirse al municipio B, al revizar los productos y contejando con la pecosa se dieron cuanta que enAl conjunto de proposiciones, conectivos lógicos y símbolos de agrupación lo denominamos fórmula lógica Por ejemplo ~{ (p ® q) Ù (s Ù t) } Si al evaluar una fórmula lógica, resulta que todos los valores de verdad resultantes son siempre V para cualquier combinación de sus valores de verdad, decimos que dicha fórmula es una Tautología o Ley lógica




Reglas De Inferencia Docsity



Propiedades De Las Proposiciones Logicas Ley Conmutativa By Freddy Gonzalo Rivera Becerra
Propiedad y ejemplo a) pq=qp Recibe ahora mismo las respuestas que necesitas! ((p → q)∧¬q) → ¬p p → q ¬q ¬p ((p → q)∧¬q) ⊢ ¬p En el lenguaje natural se lee de la siguiente manera "si p implica q, y q es falso, entonces p también es falso" Comprobación escribir cada una de las leyes lógicas de diferentes maneras y utilizando las tablas lógicas comprobar que son tautologías 14Sean p y q proposiciones La conjunción de p y q denotado p∧∧∧∧q es la proposición p y q Si p 1 1 = 3 q Un decenio tiene 10 años La conjunción de p y q es p∧q 1 1 = 3 y un decenio tiene 10 años La tabla de verdad es p q p∧∧∧∧q V V V V F F F V F F F F Lógica Matemática Cont Sean p y q proposicionesDisjunción




Logotipo De La Letra De Pq Pq Con El Ejemplo Rosado Azul Roto Quebrado Del Vector Del Diseno De La Textura De Los Triangulos Ilustraciones Vectoriales Clip Art Vectorizado Libre De Derechos




Logica Matematica Si Y Solo Si Proposicion
3 EJERCICIO 607 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfa cibles ¬(p → q) p ∨ q p q ¬(p → q) p ∨ q V V F V V F V V F V F V F F F F Las dos fbfs son simultáneamente satisfacibles, ya que son V a la vez en la 2ª interpre tación EJERCICIO 608 Comprobar por tablas de verdad si las siguientes fbfs son o no simultáneamente satisfaP ∧ q que se lee "p y q", denota la conjunción de p y q Puesto que p ∧ q es una proposición, tiene un valor de verdad, que depende sólo de los valores de verdad de p y q En específico Si p y q son verdaderas, entonces p ∧ q es verdadera;Capítulo I Lógica proposicional 3 13 Operadores lógicos Negación Dada una proposición p su contraria no p es verdadera cuando aquella es falsa y se simboliza ¬p p ¬p 0 1 1 0 Conjunción o producto lógico Dadas dos proposiciones p, q, el producto lógico es la proposición molecular p y q que se simboliza (p ∧ q) p q p ∧ q 0 0 0








A Notas De Algebra Moderna
Q Este es un ejemplo de answer choices Propiedad Asociativa Elemento Neutro Propiedad Conmutativa Propiedad Asociativa SURVEY Ungraded 60 seconds Report an issue Q ¿Qué propiedad se da cuando para sumar tres números, se suman dos cualesquiera de ellos y el resultado se suma con el tercero?Si p y q son dos proposiciones, su disyunción exclusiva se escribe p ó q y se simboliza p Ú q Condicional o Implicación Material Si p y q son dos enunciados, la proposición compuesta si p entonces q se llama condicional de p y q, y se escribe p ® q Siendo la proposición p el antecedente del condicional y q el consecuente




Logica Proposicional Fidel Vera Obeso Cuestionario Sobre La Logica Como Ciencia 1 Como




Calameo Logica De Proposiciones




1 1 Proposiciones Capitulo 1 Logica Tabla De Verdad Pdf Free Download



2




Vectores



Http Zeus Inf Ucv Cl Rsoto Cursos Inf152 Cap3 Parte1 2ppt Inf152 Pdf



2




Logica Proposicional Pptx Powerpoint




Volume 14 Issue 4 19 By Chimera Innova Group Issuu



Geometria Euclidiana Jose Rodolfo Londono Calameo Downloader




Tablas De Verdad Ejercicio 3 Youtube



Www Usmp Edu Pe Estudiosgenerales Pdf I Manuales I ciclo Matematica i Pdf



Segmentos Dirigidos Matetam




Ferrater Mora Jose Logica Matematica 1992 Pdf Pdf Txt




Leyes Logicas Ejercicios Resueltos De Algebra Proposicional Pdf En 21 Ejercicios Resueltos Algebra Conmutativa




Grietas Producidas Por Un Indentador Vickers A Crn B Tin C Zrn Y D Nbn Download Scientific Diagram




Simplificacion De Proposiciones Logicas 1 Matematica Youtube



Www Karlstorz Com Cps Rde Xbcr Karlstorz Assets Assets Pdf



Cs Famaf Unc Edu Ar Pedro Introalg15 Practico3 Pdf



2




Ley Conmutativa En Tablas De Verd By Kevin Villarraga




Equivalencias Logicas Proyecto P V Q P Q Mp4 Youtube
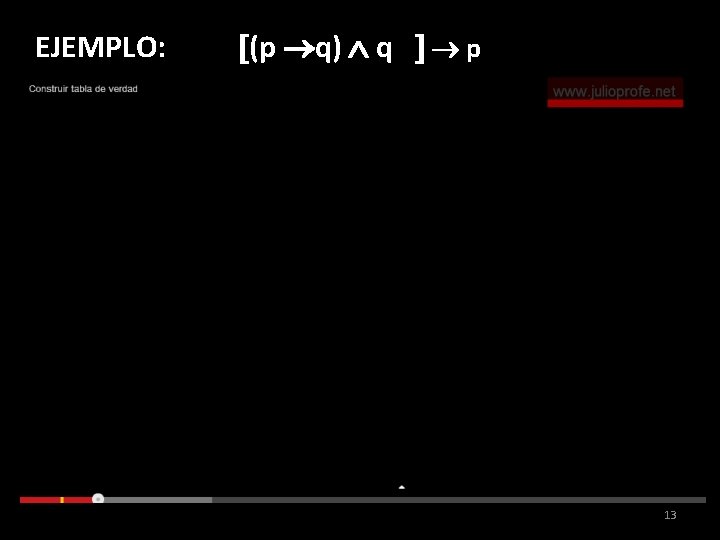



1 Proposiciones Lgicas La Lgica Proposicional O Tambin



Area De Desigualdad




1 1 Proposiciones Capitulo 1 Logica Tabla De Verdad Pdf Free Download




Logica Proposicional




Geo Trans 15 Pdf Txt




P Q Q P Propiedad Y Ejemplo Brainly Lat




Woa2 Slow Release Formulations Containing Quillay Extracts For Controlling Wheat Take All Disease Google Patents



Www Estalmat Org Archivos Cantabria V1 Pdf



Leyes Conmutativas De La Logica Proposicional By Carolina Amaya




Doc Formalizacion Y Valoracion De Proposiciones Cristhian Bacusoy Academia Edu




Logica Conjuntos Relaciones Y Funciones Pdf Descargar Libre



Http Zeus Inf Ucv Cl Rsoto Cursos Inf152 Cap3 Parte1 2ppt Inf152 Pdf



1



C Con Clase Curso De Graficos Ape2




Logica De Proposiciones Monografias Com




Conmutatividad Wikipedia La Enciclopedia Libre




Woa2 Slow Release Formulations Containing Quillay Extracts For Controlling Wheat Take All Disease Google Patents




Propiedades De La Conjuncion Y La Disyuncion By Lina Sofia Salamanca




Cap 1 Logica Y Conjuntos Modulo De Matematicas Y Fisica Snna




Logica Proposicional Pptx Powerpoint




Ejercicio De Seminario Problemas Tema 1 Logica Studocu



Www U Cursos Cl Ingenieria 16 1 Ma1101 5 Material Docente Bajar Id Material



2




1 Proposiciones Logicas La Lgica Proposicional O Tambin
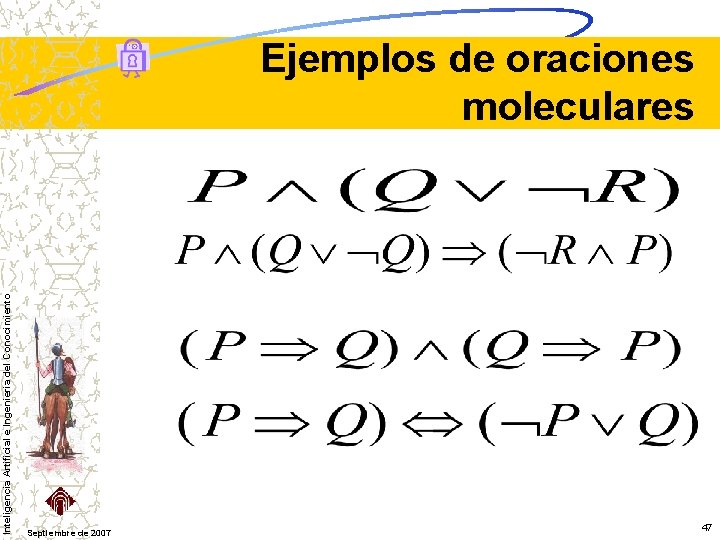



Datos De La Asignatura Temaro 2 Cuatrimestre Sistemas




Cap 1 Logica Y Conjuntos Modulo De Matematicas Y Fisica Snna




Elementos De Logica Y Teoria De Conjuntos Pdf Document




Aritmetica Teoria Ejemplos Y Problemas Marlon Arcila Yeison Gomez By Colmayor Issuu



Matematica I Calameo Downloader




Logica Proposicional Fidel Vera Obeso Cuestionario Sobre La Logica Como Ciencia 1 Como




Vectores Teorico 1



2



Www Estalmat Org Archivos Cantabria V1 Pdf




Logica Y Conjuntos Ppt Powerpoint




Tema Da 3 Logica Proposicional Calculos Logicos




Propiedades




Logica De Proposiciones Monografias Com




01 Conceptos Basicos De Logica Matematica 5




1 1 Proposiciones Capitulo 1 Logica Tabla De Verdad Pdf Free Download



2



2



Www U Cursos Cl Ciencias 11 1 Mc 110 1 Material Docente Bajar 3fid Material 3d




Lmf T1 Sintaxis Y Semantica De La Logica Proposicional Pdf Document




Ejercicios Resueltos De Logica Y Conjuntos Pdf Razonamiento Deductivo Metalogica




Como Simplificar Proposiciones Logicas Leyes Logicas Youtube




Logica Proposicional Conceptos Basicos Algebra Pre Pdf




Apunte Udec Algebra Lineal Pdf Txt



Http Www Udesantiagovirtual Cl Moodle2 Mod Resource View Php Id 14




Algebra I Unidad 1



C Con Clase Curso De Graficos Ape2



Http Bibliotecadigital Ufro Cl Actions Download Php File aa592ebceef1ee400dddc662c1e974e902d9295a4976d042dc236daec4e5c41fe8b4b1df33d9



0 件のコメント:
コメントを投稿